クックの距離(Cook’s distance)
回帰分析の診断方法の一つに、てこ比というものがあります。これをさらに拡張するとCook の距離やDFFITSといった指標に繋がります。今回はCookの距離について。
Cook の距離(Cook’s distance)
Cook の距離はアメリカの統計学者 R. Dennis Cookの名にちなみます。彼は1977年にこの概念を導入しています。[1]
Cook の距離は全てデータ用いた場合と1つのデータを除いた後求めた回帰式による予測値を用いた場合との差に関する指標です。Cook の距離が大きいと、そのデータが予測値に大きな影響を与えていることになります。つまりCook の距離が大きいデータは異常値である可能性があります。一つの基準としてCook の距離が0.5以上で影響力があり、1.0以上であると異常に大きな影響力が疑われます。
[math] \displaystyle h_{ii} [/math]をてこ比、[math] \displaystyle r_{i} [/math]を標準化残差、[math] \displaystyle n [/math]を観測データ数とした時のCookの距離[math] \displaystyle d_{i} [/math]は下記です。
[math] \displaystyle d_i =\frac {{ r }_{ i }^{ 2 }}{p+1} \left( \frac { h_{ii } }{ 1-{ h }_{ ii } } \right) [/math]
てこ比ー標準化残差プロットとCookの距離
回帰診断の方法の一つとして、横軸にてこ比、縦軸に標準化残差をプロットすることがあります。
回帰モデルのパラメータ数を[math] \displaystyle p [/math]、観測データ数を[math] \displaystyle n [/math]とすると、縦軸で[math] \displaystyle \frac{2(p + 1)}{n} [/math] より大きいデータは外れ値を疑う基準となります。また標準化誤差の基準としては絶対値が2より大きい場合はやはり外れ値を疑う基準となります。横軸/縦軸それぞれの基準を赤線で示した"てこ比-標準化残差"プロットが下記です。

前述の通りCookの距離の基準としては、0.5や1.0などが上げられます。ここではCookの距離が0.5のラインを"てこ比-標準化残差"プロットに書き込もうと思います。例えばCookの距離が0.5の場合、
[math] \displaystyle 0.5 =\frac {{ r }_{ i }^{ 2 }}{p+1} \left( \frac { h_{ii } }{ 1-{ h }_{ ii } } \right) [/math]
なので、
[math] \displaystyle { r }_{ i } = \pm \sqrt { 0.5 {(p+1)} \left( \frac { 1-{ h }_{ ii } }{ h_{ii } } \right) } [/math]
これを"てこ比-標準化残差"プロットに書き込んだものが、Fig.1の紫線です。点線が0.5、実線が1.0です。
てこ比ー標準化残差プロットのサンプル
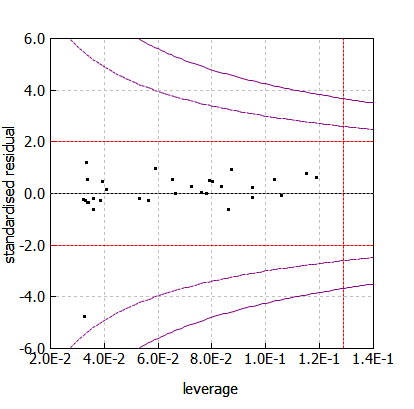
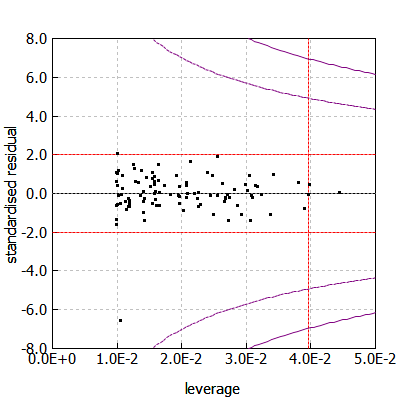
下記では[math] \displaystyle y=x [/math]の[math] \displaystyle y [/math]にノイズを加えたデータに一点だけ外れ値を混ぜています。データ数を10,30,100と3通りで、回帰直線とてこ比-標準化残差プロットを示しています。
回帰モデルのパラメータ数を[math] \displaystyle p [/math]、観測データ数を[math] \displaystyle n [/math]として、[math] \displaystyle \frac{2(p + 1)}{n} [/math] に赤縦線を外れ値のガイドとしてプロット。標準化誤差の外れ値のガイドは[math] \displaystyle \pm 2 [/math]に同様に赤横線をプロット。Cookの距離は点線が0.5、実線が1.0に書き込んでいます。
データ数が増えるにつれて、てこ比の絶対値は小さくなりますが外れ値の標準化誤差はそれほど変わりません。




まとめ
Cook の距離の計算方法と、てこ比-標準化残差プロット内での表示を説明しました。回帰分析ってツールが充実しすぎて全て理解するには時間がかかりますよね。わかれば有用だとは思います。今回も、こちらのツールに実装しています。メニューバーからDOE>Make Doehlert design fileで計画を作成できます。
[1] Cook, R. Dennis (February 1977). "Detection of Influential Observations in Linear Regression". Technometrics. American Statistical Association. 19 (1): 15–18.