主成分回帰(主成分分析)
通常の回帰分析においてXとYを入れ替えると結果が変わってしまいますが、これを避ける手法がいくつかあります。今回は2変数の場合の主成分回帰(Principal Compornent Regression, PCR)を示します。
主成分回帰の定義
主成分回帰のベースは主成分分析(Principal Component Analysis, PCA)です。主成分分析は多変量解析の一つで、多次元データの次元数を削減することができます。主成分分分析では元のデータへの寄与率が大きい変数から第n主成分と呼ばれるデータに変換します。今回考えているような2変数の回帰に当てはめると、第一主成分への回帰を考えることになります。
主成分分析に関しては解説記事が沢山あるので、イメージだけ述べます。

Fig.1にデータ例と、このデータに主成分分析を適用し求めた主成分ベクトルを点線で示します。このデータではxとyは強い相関を持っています。もし点線の座標系に変換すれば、赤点線の座標軸の成分だけ考えれば青点線の座標軸成分はノイズとして無視して良さそうです。おおざっぱに言ってしまえば、これで2変数を1変数に削減できたことになります。
この新しい座標系を求めるために、下記の分散共分散行列の固有方程式を解きます。

固有値、固有ベクトルについてもブログなどに解説記事あるので割愛。


上式を解くには、左辺の行列式を求めます。


λについて、2次方程式の解の公式を当てはめると

少し計算して


となり、固有値が大きい方から第一主成分は下記λの方になります。

次に、固有ベクトルは

を満たすので


上記の2式は行列式=0で、等価なので一つ目で考えます。


ここで第一主成分のλを代入します。

少し計算して

上式が主成分回帰での傾きになります。切片はx、yの平均を通ると下記で求められます。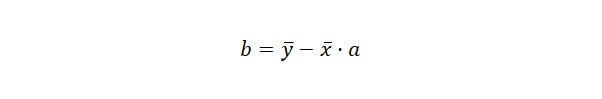
まとめ
主成分回帰の傾き、切片を求めました。主成分分析(Principal Component Analysis, PCA)では固有値、固有ベクトルを求めるので、線形代数は必須です。色々な2変数の回帰が導出できたので、そろそろ比較していきます。