回帰分析（XとYを入れ替えた場合）

XとYの関係を回帰分析で探っていると、あれ？と思うことがあります。XとYを入れ替えると結果が変わります。

XとYの入れ替え

Fig.1 (a)にXを[0,1]の乱数で、Y=XとしてYに平均0、標準偏差0.2のノイズを加えた結果を示します。Fig.1 (b)はXとYを入れ替えたものです。グラフ中に回帰分析の結果を示しています。

Fig.1 (a)では本来のY=Xに近い結果が出ており、傾き1.0353、切片-0.0178となっています。一方XとYを入れ替えただけのFig.1 (b)では同じデータにも関わらず傾き0.6664、切片0.1662と推定精度が低いことがわかります。

f:id:OceanOne:20200314012415j:plain — Fig.1 (a)Y=X, Yにノイズを加算、(b) YとXを入れ替え

同様な例でYに加えるノイズを標準偏差0.05としたものをFig.2に示します。

f:id:OceanOne:20200314013803j:plain — Fig.2 (a)Y=X, Yに標準偏差=0.05のノイズを加算、(b) YとXを入れ替え

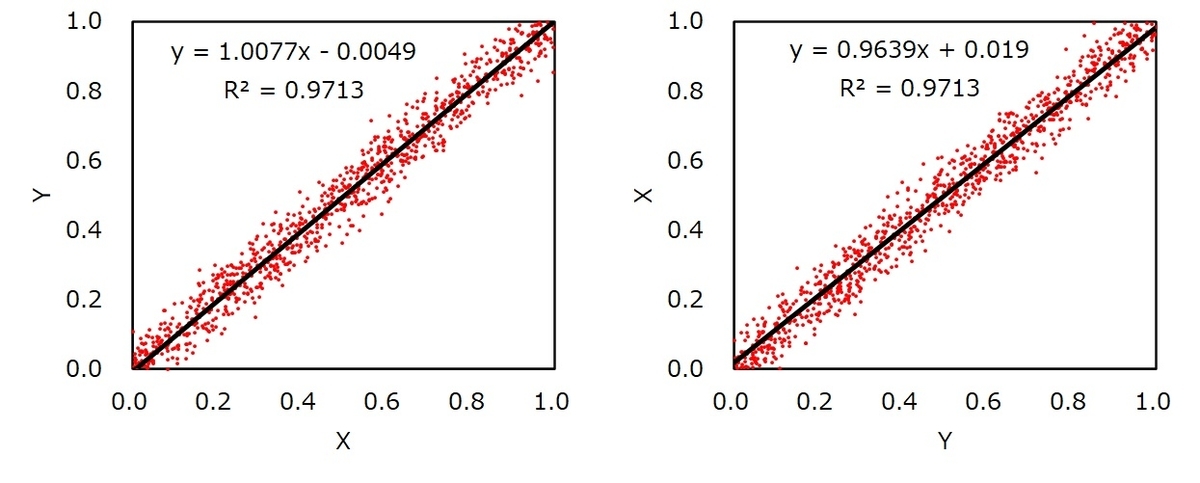
Fig.3には標準偏差0.1としたものを示します。

f:id:OceanOne:20200316000439j:plain — Fig.3 (a)Y=X, Yに標準偏差=0.1のノイズを加算、(b) YとXを入れ替え

Fig.4にFig.1を再掲します。Yへ加えたノイズの標準偏差は0.2です。

ご覧のようにY=Xとした場合の回帰分析の精度はほとんど変わらないのに、YとXを入れ替えた途端に回帰直線はズレてしまい、傾きが寝てしまいます。また入力変数へのノイズが増えるほど精度は落ちます。

最小二乗法の定義より

回帰分析を行う場合、通常最小二乗法を用いてフィッティングを行います。最小二乗法による係数の求め方は

f:id:OceanOne:20200312021646j:plain

でした。この式の意味する所はFig.5に示すように予測値と実測値の差分をY軸上で最小化することです。予測値も実測値もY軸上での事柄なので、Xへのノイズに関しては考慮していないことが分かります。

f:id:OceanOne:20200316010120j:plain — Fig.5 最小二乗法による推定方法

実務的な状況に置き換えてみます。つまり実験結果を解析する場合に、実験結果へのノイズは仮定されていますが、実験条件へのノイズは仮定されていないことになります。

例えば、温度を変化させて実験を行う場合、温度の誤差は"0"で実験結果のみがノイズを持つと仮定していることになります。

もちろん、応答変数Yに対して入力変数Xの変動が無視しうるほど小さければ、このような過程は妥当です。しかし、入力変数Xに対しても観測値を用いる場合などには、測定上の誤差などが必ず含まれます。解析を行う上で実験のバラツキを知っておくことは非常に重要です。

Xにノイズが含まれる場合

これまで述べた単純な線形回帰はOLS(Ordinary Leat Squares)と呼ばれ、説明変数Xにはノイズが含まれない事が前提です。説明変数Xにもノイズが含まれる場合の解決法として、特殊な回帰が提案されています。標準主軸回帰（Standardised Major Axis[SMA]、幾何平均回帰、Geometric Mean[GM]）、主成分回帰(PCR)、Deming回帰、Passing-Bablok回帰(PB)、などです。

標準主軸回帰（幾何平均回帰）は二つの一次回帰（y on x, x on y）の傾きの幾何平均、主成分回帰は回帰直線への距離^2を最小化、Deming法はX、Yそれぞれへの誤差比に関する主成分回帰の一般化、Passing-Bablok法はすべての２点間の傾きの中央値に基づくロバストな回帰になります。

下記にはFig.4-(b)（Y=X、Xに標準偏差=0.2のノイズ）のデータについて、OLS、SMA、PCR、PBの4手法における回帰結果を示します。SMAもPCRもXへのノイズに対するロバスト性が高いことがわかります。PBはOLSとSMA/PCRの中庸な結果ですが、重要な点は外れ値へのロバスト性だと思います。（今回のデータからはわかりません）